Dividing Polynomials by Monomials and Binomials
Dividing a Polynomial by a Monomial
We know how to divide some simple polynomials by monomials. For example,
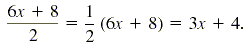
We use the distributive property to take one-half of 6x and one-half of 8 to
get 3x + 4. So both 6x and 8 are divided by 2. To divide any polynomial by a
monomial, we divide each term of the polynomial by the monomial.
Example 1
Dividing a polynomial by a monomial
Find the quotient for (-8x6 + 12x4 - 4x2)
÷ (4x2).
Solution
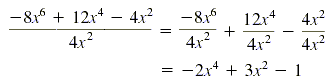
The quotient is -2x4 + 3x2 - 1. We can check by
multiplying.
4x2(-2x4 + 3x2 - 1) = -8x6 + 12x4
- 4x2.
Because division by zero is undefined, we will always assume that the divisor
is nonzero in any quotient involving variables. For example, the division in
Example 1 is valid only if 4x2 ≠ 0, or
x2 ≠ 0.
Dividing a Polynomial by a Binomial
Division of whole numbers is often done with a procedure called long division.
For example, 253 is divided by 7 as folows:
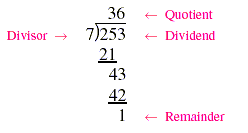
Note that 36 · 7 + 1 = 253. It is always true that
(quotient)(divisor) + (remainder) = (dividend).
To divide a polynomial by a binomial, we perform the division like long
division of whole numbers. For example, to divide x2 - 3x - 10 by x +
2, we get the first term of the quotient by dividing the first term of x + 2
into the first term of x2 - 3x - 10. So divide x2 by x to
get x, then multiply and subtract as follows:
| 1) Divide: 2) Multiply:
3) Subtract: |
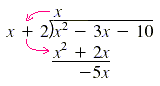 |
x2 ÷ x = x
x · (x + 2) = x2 + 2x
-3x - 2x = -5x |
Now bring down -10 and continue the process. We get the second term of the
quotient (below) by dividing the first term of x + 2 into the first term of -5x
- 10. So divide -5x by x to get -5:
| 1) Divide: 2) Multiply:
3) Subtract: |
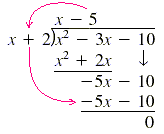 |
-5x ÷ x = -5
Bring down -10.
-5(x + 2) = -5x - 10
-10 - (-10) = 0 |
So the quotient is x - 5, and the remainder is 0.
In the next example we must rearrange the dividend before dividing.
Example 2
Dividing a polynomial by a binomial
Divide 2x3 - 4 - 7x2 by 2x - 3, and identify the
quotient and the remainder.
Solution
Rearrange the dividend as 2x3 - 7x2 - 4. because
the x-term in the dividend is missing, we write 0 · x for it:
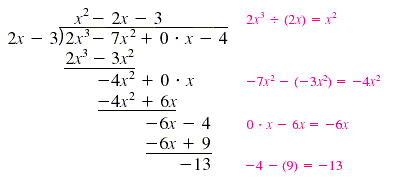
The quotient is x2 - 2x - 3, and the remainder is -13. Note that
the degree of the remainder is 0 and the degree of the divisor is 1. To check,
we must verify that
(2x - 3)(x2 - 2x - 3) - 13 = 2x3 - 7x2
- 4.
Caution
To avoid errors, always write the terms of the divisor and the dividend
in descending order of the exponents and insert a zero for any term that is
missing.
If we divide both sides of the equation
dividend = (quotient)(divisor) + (remainder)
by te divisor, we get the equation

This fact is used in expressing improper fractions as mixed numbers. For
example, if 19 is divided by 5, the quotient is 3 and the remainder is 4. So
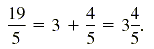
We can also use this form to rewrite algebraic fractions.
|