|
TUTORIALS:
|
Graphing an Inverse Function
If a function f has an inverse f -1, you can use the graph of f to find the
graph of f -1.
Procedure — To Graph the Inverse of a Function
Step 1 Identify several points (a, b) on the graph of the given
function.
Step 2 Switch the x- and y-coordinates of each point to form the
points (b, a) for the inverse function.
Step 3 Plot the new points and connect them with a smooth line.
Note:
Remember, if f contains the ordered pair
(a, b), then f -1 contains the ordered pair
(b, a).
Example 1
The graph of f(x) = 2x - 5 is shown. Graph f -1.
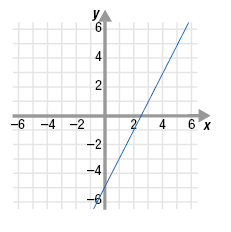
Solution
Step 1 Identify several points (a, b) on the
graph of the given function.
From the graph, we choose (0, -5), (1, -3), and (4, 3).
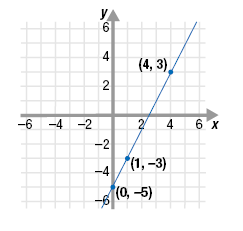
Step 2 Switch the x- and y-coordinates of
each point to form the points (b, a)
for the inverse function.
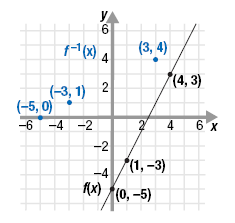
The new ordered pairs are (-5, 0), (-3, 1), and (3, 4).
Step 3 Plot the new points and connect
them with a smooth line
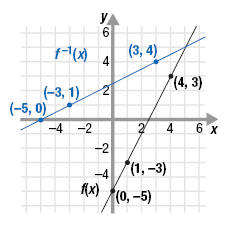
There is a visual relationship between the graphs of a function and its
inverse function. To see this, let’s start with the graphs of f and f -1
from
the last example. Look at what happens when we add the graph of y = x.
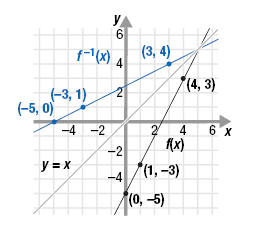
Notice that the graphs of f and f -1 are symmetric about the line y = x.
That is, f -1 is the reflection of f about the line y = x. Similarly, f is the
reflection of f -1 about the line y = x.
Note:
If the point (a, b) is on the graph
of f, then its mirror image (b, a) is
on the graph of f -1.
So, one way to get the graph of f -1 is to
start with the graph of f, and reflect it
about the line y = x.
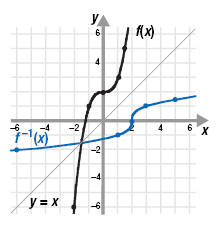
Example 2
The graph of f(x) is shown. Graph f -1.
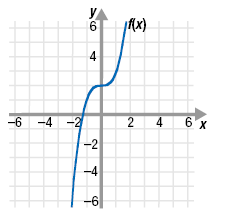
Solution
Step 1 Identify several points (a, b) on the
graph of the given function.
From the graph, we choose (-2, -6), (-1, 1), (0, 2), (1, 3), and (1.4, 5).
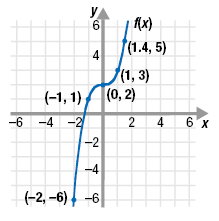
Step 2 Switch the x- and y-coordinates of
each point to form the points (b, a)
for the inverse function.The new ordered pairs are (-6, -2), (1, -1), (2, 0), (3, 1) and
(5, 1.4).
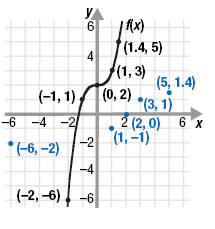
Step 3 Plot the new points and connect
them with a smooth line.
Notice that f and f -1 are symmetric about the line y = x.
|