|
TUTORIALS:
|
Fractions
900000 ÷ 300 = ? 30 ÷ 100 = ?
Write 900,000 ÷ 300 as 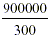 . We are used to seeing the divided –
often called the numerator - above the fraction line and the
divider (or denominator) below the fraction line. We can write
900000 as 9 × 100000 and 300 as 3 × 100. The task then looks
like . We are used to seeing the divided –
often called the numerator - above the fraction line and the
divider (or denominator) below the fraction line. We can write
900000 as 9 × 100000 and 300 as 3 × 100. The task then looks
like 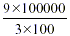 . .
Let us first consider 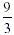 , which equals 3. We should have divided
something 100000 time bigger than 9, making the result 100000
times bigger. We should also have divided by something 100 times
bigger than 3, making the result 100 times smaller. What results
from making something 100000 times bigger and then 100 times
smaller? You can think of the latter as 10 times smaller and then
10 times smaller again, each time knocking one 0 off the 100000,
leaving 1000 as the net 'adjustment' to the 3. , which equals 3. We should have divided
something 100000 time bigger than 9, making the result 100000
times bigger. We should also have divided by something 100 times
bigger than 3, making the result 100 times smaller. What results
from making something 100000 times bigger and then 100 times
smaller? You can think of the latter as 10 times smaller and then
10 times smaller again, each time knocking one 0 off the 100000,
leaving 1000 as the net 'adjustment' to the 3.
So 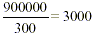 . .
In the same way, 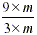 is just is just 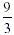 because
there is the same m -fold increase as the m-fold decrease. Note
that this does not work with, for example, because
there is the same m -fold increase as the m-fold decrease. Note
that this does not work with, for example, 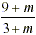 (Try
taking m = 3 which gives (Try
taking m = 3 which gives 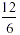 which is 2, not 3). In the case of 30 ÷
100, (i.e. 30 %), again we start with which is 2, not 3). In the case of 30 ÷
100, (i.e. 30 %), again we start with 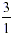 and then
make it ten times bigger (because the divided is 30, not 3) and
one hundred times smaller (because the divider is 100, not 1).
The net adjustment is 10 times smaller than the 3, namely 0.3 and then
make it ten times bigger (because the divided is 30, not 3) and
one hundred times smaller (because the divider is 100, not 1).
The net adjustment is 10 times smaller than the 3, namely 0.3
Remember: The correct value of a fraction can also always be
found by long division.
|