|
TUTORIALS:
|
Rational Exponents
Definition —
Rational Exponent With Numerator m
If a is a real number, m is a nonnegative integer, n is a positive
integer, and
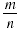 is in lowest terms, then
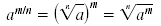
If n is even, then am/n is a real number only when a
≥ 0.
Examples:
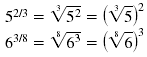
Note:
When m = 1, we have
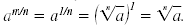
That is
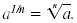
Example 1
Rewrite using a radical and evaluate: 323/5
Solution
We will use three different methods to solve this problem.
Method 1 Use
 |
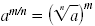323/5 |
| Here, a = 32, m = 3, and n = 5. |
 |
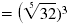| Find the prime factorization of 32.
32 = 2 · 2
· 2 · 2
· 2 = 25. |
 |
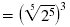| Simplify the radical.
Evaluate 23. |
= (2)3 = 8 |
Method 2 Use
 |
|
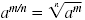| Comparing am/n to 323/5 we see that a
= 32,
m = 3, and n = 5. |
 |
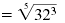| Use your calculator to find 323. |
 |
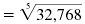Use your calculator to find
 |
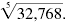= 8 |
| Method 3 Use the Power of a Power Property
of Exponents, (am)n = amn.
|
323/5 |
| Find the prime factorization of 32.
32 = 2 · 2
· 2 · 2
· 2 = 25. |
= (25)3/5 |
| Use the Power of a Power Property of Exponents.
|
 |
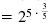| Multiply the exponents and write the result
in lowest terms.
Evaluate 23. |
= 23
= 8 |
In summary, all three methods lead to the same result: 323/5
= 8
Note:
Method 2 typically means dealing with
larger numbers since we first evaluate the
power.
|
