|
TUTORIALS:
|
Rationalizing the Denominator
Square roots such as
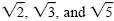 are irrational numbers. If roots of this type
appear in the denominator of a fraction, it is customary to rewrite the fraction with
a rational number in the denominator, or rationalize it. We rationalize a denominator
by multiplying both the numerator and denominator by another radical that
makes the denominator rational. are irrational numbers. If roots of this type
appear in the denominator of a fraction, it is customary to rewrite the fraction with
a rational number in the denominator, or rationalize it. We rationalize a denominator
by multiplying both the numerator and denominator by another radical that
makes the denominator rational.
You can find products of radicals in two ways. By definition,
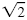 is the positive
number that you multiply by itself to get 2. So is the positive
number that you multiply by itself to get 2. So
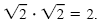
By the product rule,
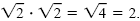 Note that Note that
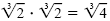 by the
product rule, but by the
product rule, but
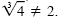 By definition of a cube root, By definition of a cube root,
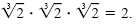
Example 1
Rationalizing the denominator
Rewrite each expression with a rational denominator.

Solution
a) Because
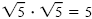 , multiplying both the numerator and denominator
by , multiplying both the numerator and denominator
by
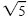 will rationalize the denominator: will rationalize the denominator:
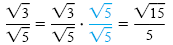 |
By the product rule,
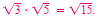 |
b) We must build up the denominator to be the cube root of a perfect cube. So we
multiply by
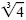 to get to get
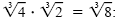
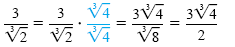
Caution
To rationalize a denominator with a single square root, you
simply multiply by that square root. If the denominator has a cube root, you build
the denominator to a cube root of a perfect cube, as in Example 1(b). For a fourth
root you build to a fourth root of a perfect fourth power, and so on.
Helpful hint
If you are going to compute
the value of a radical expression
with a calculator, it doesn’t
matter if the denominator
is rational. However, rationalizing
the denominator provides
another opportunity to practice
building up the denominator
of a fraction and
multiplying radicals.
|