|
TUTORIALS:
|
Simplifying Radicals
When simplifying any expression, we try to make it look “simpler.†When simplifying
a radical expression, we have three specific conditions to satisfy.
Simplified Radical Form for Radicals of Index n
A radical expression of index n is in simplified radical form if it has
1. no perfect nth powers as factors of the radicand,
2. no fractions inside the radical, and
3. no radicals in the denominator.
The radical expressions in the next example do not satisfy the three conditions for
simplified radical form. To rewrite an expression in simplified form, we use the product
rule, the quotient rule, and rationalizing the denominator.
Example 1
Writing radical expressions in simplified radical form
Simplify.
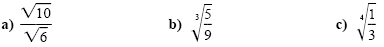
Solution
a) To rationalize the denominator, multiply the numerator and denominator by
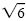 : :
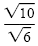 |
 |
Rationalize the denominator. |
| |
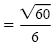 |
|
| |
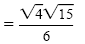 |
Remove the perfect square from
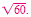 |
| |
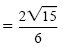 |
|
| |
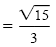 |
Reduce
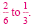 Note that Note that
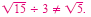 |
b) To rationalize the denominator, build up the denominator to a cube root of a
perfect cube. Because
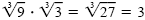 , we multiply by , we multiply by
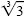 : :
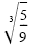 |
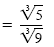 |
Quotient rule for radicals |
| |
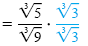 |
Rationalize the denominator. |
| |
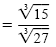 |
|
| |
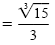 |
|
c) To rationalize the denominator, observe that
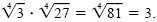
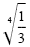 |
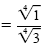 |
Quotient rule for radicals |
| |
 |
Rationalize the denominator. |
| |
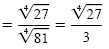 |
Do not omit the index of the radical in any step. |
|