|
TUTORIALS:
|
Adding and Subtracting Fractions
You can always add or subtract fractions using common
denominators. To find common denominators, you need to first find
the least common multiple of all the denominators involved. This
can be sometimes be difficult. There is an easier method for
adding or subtracting fractions without finding a common
denominator.
Adding Fractions using Cross Multiplication
Cross multiplication refers to the multiplication of the
numerator from one fraction and the denominator of another. The
following example is worked using cross multiplication.
Example:
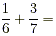
Here is how cross multiplication works: You multiply 1 × 7
and 6 × 3 then add these two products together. The new
denominator for the sum is the product 6 × 7.
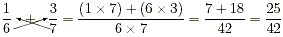
Therefore,  .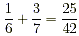
There are some problems where it might be easier for you to
use common denominators, like 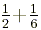 , however, in general, you will save time using the
cross multiplication method. If the least common denominator of
the two fractions is not the product of the two denominators,
then you are going to have to reduce the fraction when you are
finished. Be prepared for that situation by not writing anything
down until you finish the entire problem. However, when the two
denominators differ by only one, the least common denominator for
those two fractions is going to be the product of the two
denominators. Using algebraic notation, the cross multiplication
method for addition is
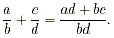
Subtracting Fractions using Cross Multiplication
The method is virtually the same with subtracting fractions.
The only change is that instead of adding, you now subtract the
two products. In this case, the order does matter.
Example:
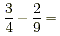
Use cross multiplication and subtract (3 × 9)-(4 × 2) from
the numerator.
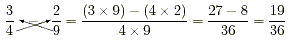
Thus,  .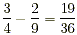
Using algebraic notation, the cross multiplication method for
subtraction is
|
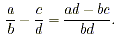
