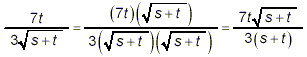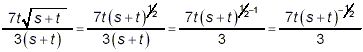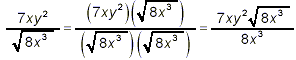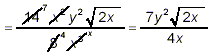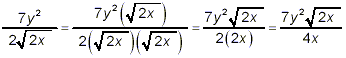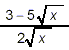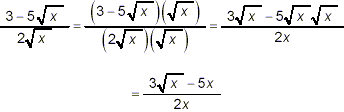|
Home |
Rationalizing the DenominatorExamples with Solutions
Example 1: Simplify solution: There is no factorization of the expression in the square root possible here, so the only simplification necessary is to rationalize the denominator of the fraction. Since the square root in the denominator is already as simple as possible, we need to just multiply the numerator and denominator by that square root to achieve the required result.
Although there is a t in both the numerator and the denominator, it is not a factor in the denominator, and therefore we cannot cancel the t’s between the numerator and denominator of this last form. In fact, there is obviously no common factors to cancel between the numerator and denominator of this last form, so this last expression is as simple as possible and so it must be the required final answer. NOTE: Sometimes as they focus on simplifying fractions such as the final result of Example 1 above, people note that the numerator and denominator contain a power of the same expression – in this case of (s + t). Without thinking they do the following:
or
Superficially, it may appear that one or both of these lines represents a useful simplification, but in fact, both lines really just amount to reversing the simplification previously done. The second line obviously just gives back the original problem, and the first line does as well, though in a somewhat less recognizable form. So, while it is very useful to break the simplification of complicated algebraic expressions down into a series of relatively simple independent steps, it is also important to review your entire solution to make sure that you haven’t lost track of what the problem actually requires you to accomplish, and make sure that that is indeed what your final answer has accomplished.
Example 2: Rationalize the denominator in solution: If we simply follow the steps illustrated in the first and second examples above, we get
which has a rational denominator, but clearly can be simplified further. First 8x 3 = 2 2 · 2 · x 2 · x so
Thus,
as the final simplified result. Alternatively, we could have noted that the square root in the denominator of the original fraction is not in simplest form, and so we could have started by simplifying both the square root and the fraction itself first:
Now the denominator of this fraction can be rationalized by
multiplying the numerator and denominator by
giving the same final simplified result as we obtained earlier.
Example 3: Simplify solution: No common factors can be found to cancel between the numerator
and denominator here. Also, the square roots which appear here
obviously cannot be simplified further. So, all that’s left
to do to simplify this expression is to rationalize the
denominator. This is accomplished by multiplying the numerator
and denominator by
as the final result (since there are clearly no common factors
that can be cancelled between the numerator and denominator of
this final expression). Notice that we used brackets explicitly
to ensure that the entire numerator was multiplied by |