|
TUTORIALS:
|
Simplifying Products and Quotients Involving Square Roots
The basic strategy here is to simplify any square roots that
remain after the two expressions involving square roots are
multiplied, or after one is divided by another. The
simplification is assisted by removing perfect squares from the
square roots, as illustrated previously in these notes.
Example:
Simplify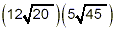 
solution:
We could start by simply multiplying the coefficients and
multiplying the square roots to get
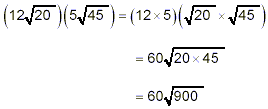
Now check to see if the square root can be simplified.
Checking for perfect square factors in 900, we see immediately
that
900 = 9 × 100 = (3 2 ) × (10 2 )
So
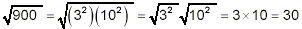
Hence
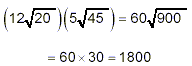
as the simplest form (with no square root at all remaining).
We could also have attempted to simplify the original square
roots first before multiplying. This would have first given:
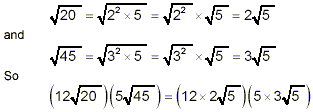
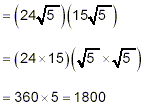
since 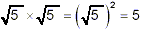 . We got the same final
result, of course using both methods.
Example:
Simplify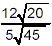 
solution:
In the case of division (or a quotient), it is usually more
efficient to simplify the two square roots first. So here, we
have
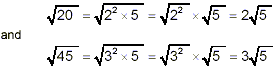
So, now we can write
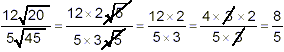
We were able to cancel common factors in the numerator and
denominator to reduce the final result to the simplest form
indicated. This method of simplification of fractions is
described and illustrated at greater length in the section of
these notes dealing with fractions.
|
