|
TUTORIALS:
|
Solving Quadratic Equations by Completing the
Square
Now, we will complete the square to solve a quadratic equation.
| For example, let’s solve: |
x2 + 2x = 4 |
We begin on the left-side of the equation by completing the square.
To find the number needed to complete
the square for x2 + 2x, calculate
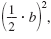 where b
= 2. where b
= 2. |
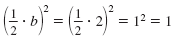 |
Thus, to complete the square for x2 + 2x, we add 1.
| However, we are working with an
equation, so we must add 1 to both
sides of the equation.
|
x2 + 2x + 1 |
= 4 + 1 |
| The left side can be written as the
square of a binomial. |
(x + 1)2 |
= 5 |
| To solve this equation, use the
Square Root Property:
|
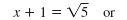 |
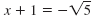 |
| For each equation, subtract 1
from both sides. |
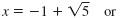 |
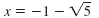 |
So, the two solutions of x2 + 2x = 4 are
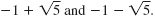
We can write the solutions using shorthand notation:
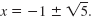
Here is a procedure we can use to solve any quadratic equation.
Note:
The symbol ± is read “plus or minus.â€
Procedure — To Solve a Quadratic Equation by Completing the Square
Step 1 Isolate the x2-term and the x-term on one side of the
equation.
Step 2 If the coefficient of x2 is not 1, divide both sides of the
equation by the coefficient of x2.
Step 3 Find the number that completes the square:
• Multiply the coefficient of x by
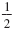 . .
• Square the result.
Step 4 Add the result of Step 3 to both sides of the equation.
Step 5 Write the trinomial as the square of a binomial.
Step 6 Finish solving using the Square Root Property.
Step 7 Check each solution.
|