Rationalizing the Denominator
Examples with Solutions
Example 1:
Simplify 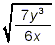
solution:
Since it is a basic property of radicals that
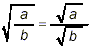
we see that the given expression actually amounts to a
fraction with a radical in the denominator. Therefore, to
accomplish simplification of this expression, we need to
rationalize the denominator:

A quick check before moving on indicates that there is a
perfect square factor in the square root that remains, and so we
remove this factor from the square root before declaring a final
answer:
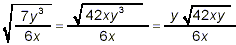
There really is nothing else we can do to this final
expression to simplify it further, so it must be the required
final answer.
Example 2:
Write the result of the following division in simplified form:
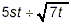
solution:
We deal with division involving radicals in detail in a later
document in this series. However, you are already familiar with
the way fractions express division, so that here we can write
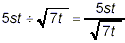
The only possible simplification at this stage is to
rationalize the denominator, which can be accomplished by
multiplying the numerator and denominator by 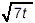 : :
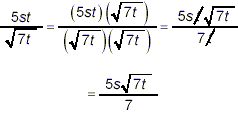
as the required simplest final result.
Example 3:
Write the result of the following division in simplest form:
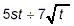
solution:
This example is very similar to the previous Example 6, and so
you should use it as a practice problem. Attempt to work out the
final answer yourself before looking at the steps of our
solution, which follows.
Here
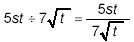
Now, we rationalize the denominator by multiplying the
numerator and denominator by 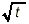 to get to get
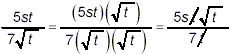
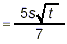
as the required final answer in simplified form.
Example 4:
The formula for the area, A, of a circle of radius r is given
by
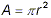
Derive a formula for the radius, r, in terms of the area, A,
and make sure that your result satisfies the usual criteria of
simplicity.
solution:
We deal systematically with the topic of rearranging formulas
in another document on this website. However, we can handle this
problem without having to invoke a general strategy. Since
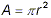
we can write
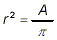
by just dividing both sides of the original formula by 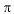 . Now we have a formula for r 2. To get a
formula for r, we need to take the square root of both sides: . Now we have a formula for r 2. To get a
formula for r, we need to take the square root of both sides:
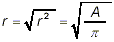
This formula looks quite simple already, but it does consist
of the square root of a fraction, and so the usual rules of
simplification say we should rationalize the denominator. This is
easily done:

Thus, the final simplified formula for r is
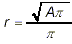
|