|
TUTORIALS:
|
Solving Equations with Fractions
After studying this lesson, you will be able to:
- Solve equations containing fractions.
To Solve Equations containing fractions:
Clear out the fractions by multiplying the ENTIRE equation by
the common denominator.
SPECIAL CASES
Sometimes when dealing with equations, all the variable cancel
out. When this happens we have a "special case". If the
expression we're left with is a true mathematical statement, our
solution is called the Identity Property which
means that there is an infinite number of solutions. The symbol
for infinity is 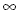 . If the expression we're left with is a false
mathematical statement, there will be no solution. We indicate
this with the empty set symbol which is Ø.
Example 1
| 2x + 5 = 2x -3 |
To solve this equation, we need to
attempt to get the variables together on the same side. |
| 2x + 5 - 2x = 2x -3 - 2x |
When we subtract 2x from each side, all
variables are eliminated, leaving us with 5 = -3 |
| 5 = -3 |
We know this is a "special
case" since we have no variables. Since 5 is not
equal to -3, this is a false statement. Therefore there
are no solutions. |
| Ø |
We write the empty set symbol for our
answer |
Example 2
| 3 ( x + 1 ) - 5 = 3x -2 |
To solve this equation, we first remove
the parentheses by distributing. |
| 3x + 3 - 5 = 3x - 2 |
We need to collect like terms (3 - 5 ) on
the left side |
| 3x - 2 = 3x -2 |
To solve this equation, we need to
attempt to get the variables together on the same side. |
| 3x - 2 - 3x = 3x -2 - 3x |
We do this by subtracting 3x from each
side. This gives us -2 = -2
|
| -2 = -2 |
We know this is a "special
case" since we have no variables. Since -2 is equal
to -32, this is a true statement (the identity property).
Therefore there are infinite number of solutions. |
|
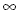We write the symbol for infinity for our
answer |
|
